Penjelasan dan Contoh Soal Himpunan Semesta dan Himpunan Kosong

Dalam pembahasan matematika, himpunan adalah kumpulan objek yang dapat dikelompokkan menjadi suatu kesatuan serta memiliki sifat-sifat yang dapat didefinisikan dengan jelas. Kelompok atau himpunan para ayah yang hobi bersepeda, atau himpunan siswi yang tinggi badannya di atas 150 centimeter, adalah contoh dari penggunaan konsep himpunan. Pembahasan himpunan berkaitan erat dengan pengelompokan objek-objek.

Apakah objek-objek tertentu termasuk dalam suatu kelompok, termasuk dalam kelompok lainnya, termasuk atau tergolong dalam beberapa kelompok sekaligus (beririsan), atau bahkan berada di luar kelompok atau tidak termasuk suatu himpunan? Apa sajakah keseluruhan objek yang kita diskusikan atau amati? Hal-hal di atas menjadi bahan diskusi mengenai himpunan.

Dalam pembahasan ini kita akan berkenalan dengan dua konsep dalam diskusi himpunan yakni Himpunan Semesta dan Himpunan Kosong. Bagaimanakah kita dapat memahami dan mengenali himpunan semesta dan himpunan kosong dalam kehidupan sehari-hari? Mari kita ikuti penjelasan selengkapnya.

 

Himpunan Semesta, Pembicaraan yang Mendahului Pengelompokkan

Himpunan semesta secara sederhana dapat diartikan himpunan yang anggotanya semua objek yang sedang dibicarakan. Sebagai contoh, himpunan vokal (huruf hidup) = {A, E, I, O, U}, dalam contoh ini semua anggota yang merupakan vokal sudah diidentifikasikan seluruhnya himpunan semestanya adalah S = {huruf vokal} . 

Contoh lainnya, himpunan bilangan prima yang lebih dari 4 dan kurang dari 20, anggotanya adalah {5, 7, 11, 13, 17, 19}, Himpunan semestanya bisa jadi S = {bilangan asli}.

Lantas bagaimanakah hubungan dan perbedaan antara himpunan semesta dengan himpunan bagian atau himpunan lainnya? Mari kita membahas lebih lanjut.

    Di dalam sebuah kotak pensil terdapat sejumlah benda yakni pulpen, pensil, penghapus, penggaris, dan busur derajat. Jika kita diminta menyebutkan mana sajakah benda dalam kotak pensil tersebut yang dapat digunakan untuk menulis, maka dengan cukup mudah kita dapat memberikan jawaban, pensil dan pulpen.

 

   Tahukah kamu bahwa dari cerita di atas kita telah berjumpa dengan himpunan semesta? Mari kita membahasnya kembali.

 

Jawaban berupa pensil dan pulpen tadi merupakan anggota himpunan benda dalam kotak pensil yang dapat digunakan untuk menulis, atau, dengan memberi nama himpunan tadi sebagai A, maka dapat pula kita tuliskan sebagai berikut:

A = {pensil, pulpen}

Namun jika kita perhatikan lebih seksama, sebelum pengelompokkan tersebut, atau sebelum kita menentukan himpunan A dan anggota-anggotanya, pembicaraan kita awali dengan kata-kata sebagai berikut:

“Di dalam sebuah kotak pensil terdapat sejumlah benda yakni …”

Pembicaraan ini kita awali dengan sebuah kotak pensil dan inilah Himpunan Semesta dalam pembicaraan kita. Lambang yang biasanya digunakan untuk menyatakan himpunan semesta adalah “S ”. Dalam contoh ini, semua benda yang ada di dalam kotak pensil menjadi anggota himpunan semesta yakni pen, pensil, penghapus, penggaris, dan busur derajat. Sehingga secara matematis, himpunan semesta dari contoh di atas dapat dituliskan sebagai berikut:

S = {isi kotak pensil}

 

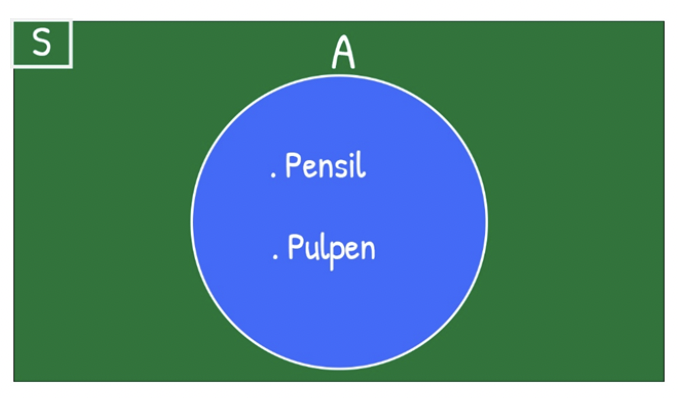
Hubungan antara himpunan semesta dan himpunan A dari contoh di atas dapat dipahami dengan mengamati diagram Venn di samping ini: Dari diagram di atas kita dapat memahami bahwa himpunan A adalah himpunan bagian dari himpunan semesta. 

Kita dapat pula membuat himpunan lainnya untuk mengelompokkan anggota-anggota himpunan semesta ini, misalnya, kita bisa mendefinisikan himpunan B sebagai himpunan isi kotak pensil yang berupa alat ukur, dan dengan demikian kita dapat menyebutkan anggota himpunan B yakni penggaris dan busur derajat. Secara matematis, himpunan B dapat dinyatakan sebagai berikut:

 B = {penggaris, busur derajat}

Dalam hal ini pun, himpunan B merupakan himpunan bagian dari himpunan semesta, dimana anggota himpunan B merupakan anggota himpunan semesta yang memenuhi definisi atau ketentuan untuk menjadi anggota himpunan B (alat ukur).

Apakah gabungan anggota semua himpunan yang sedang kita bahas dalam suatu soal atau pertanyaan adalah merupakan himpunan gabungan (union)? Belum tentu. Perhatikanlah ilustrasi berikut ini. Jika kita memiliki 4 himpunan yakni A, B, C, D dengan masing-masing anggotanya sebagai berikut

A = {1, 3, 5}

B = {2, 4, 6}

C = {1, 2, 3, 4, 5, 6}

D = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}

manakah dari keempat himpunan di atas yang paling tepat sebagai himpunan semesta?

 

Pembahasan:

Kita dapat membuat diagram Venn seperti nampak di bawah ini

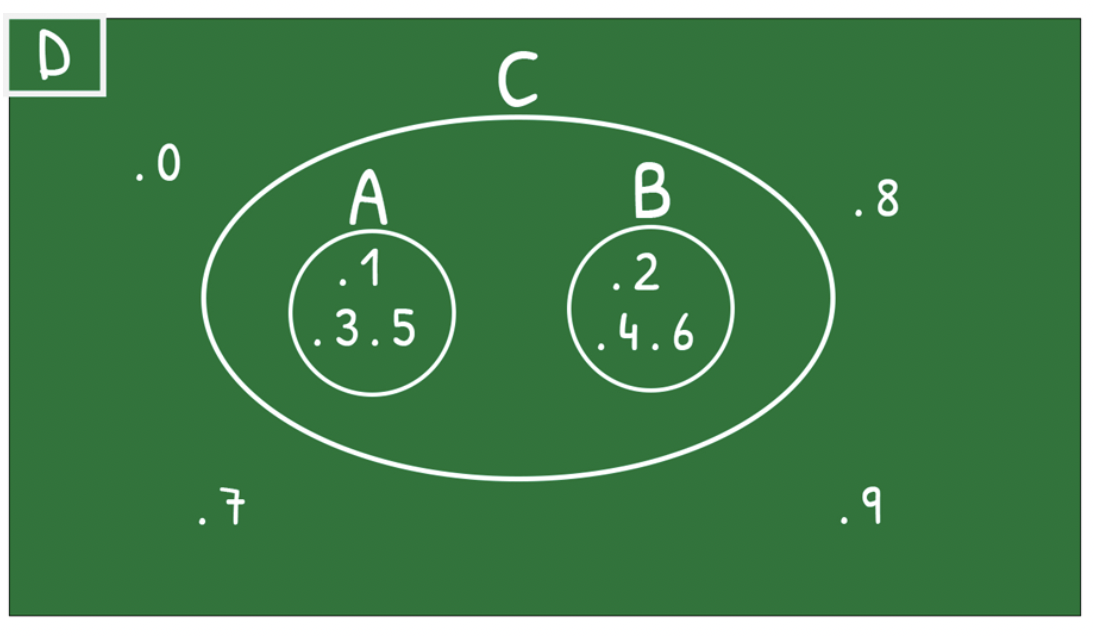
Dari diagram ini kita dapat melihat bahwa himpunan A dan B terpisah satu sama lain, karena mereka masing-masing tidak mengandung anggota yang merupakan keseluruhan objek yang sedang kita bicarakan, maka baik himpunan A maupun B bukanlah himpunan semesta. 

Bagaimana dengan himpunan C? Himpunan C merupakan himpunan yang beranggotakan seluruh anggota himpunan A dan seluruh anggota B. Dengan demikian himpunan C merupakan himpunan gabungan (union) antara himpunan A dan B. Namun karena masih ada bilangan-bilangan lain yakni 0, 7, 8 dan 9 yang tidak termasuk anggota himpunan C, maka himpunan C belum mencakup seluruh objek pembicaraan, dengan kata lain, himpunan C bukanlah himpunan semesta. 

Sebelum kita menapak pada himpunan semesta, ada baiknya kita juga memahami mengenai himpunan komplemen. Jika ada bagian dari himpunan semesta yang tidak termasuk anggota suatu himpunan (dalam hal ini kita gunakan himpunan C sebagai contoh), maka himpunan komplemen dari C (diberi simbol C’) akan memiliki anggota yang merupakan bagian dari himpunan semesta yang tidak termasuk anggota C, yakni 0, 7, 8 dan 9. Maka himpunan komplemen C dapat dituliskan sebagai berikut:

 C’={0,7,8,9}

Lalu bagaimanakah dengan himpunan D. Nah, himpunan D memiliki anggota juga merupakan seluruh anggota himpunan C dimana C = A U B, dan selain itu pula, himpunan D memiliki anggota yang tidak termasuk anggota himpunan C. Dengan demikian D memiliki anggota berupa semua bilangan atau objek yang sedang kita bicarakan. Dengan demikian D = S, atau D merupakan himpunan semesta dalam persoalan atau pembicaraan tersebut.

Nah, dapatkah kamu menyebutkan contoh-contoh himpunan semesta lainnya?

 

Himpunan Kosong, Kelompok Sekadar Nama Tanpa Anggota

Sebutkan anggota himpunan nama-nama hari yang di dalamnya memiliki huruf “z”, himpunan nama bulan yang memiliki 32 hari, atau himpunan nama burung yang berkembang biak dengan cara melahirkan. Setelah kamu mencoba tentu kamu akan tiba pada kesimpulan bahwa ketiga himpunan tersebut tidak memiliki anggota yang dapat diidentifikasi dan disebutkan.

Himpunan Kosong adalah himpunan yang tidak memiliki anggota apapun. Dalam himpunan kosong, tidak ada objek yang dapat diidentifikasikan, tidak ada objek yang dapat memenuhi kondisi atau syarat himpunan tersebut. Himpunan kosong biasanya dituliskan sebagai berikut:

A = Ø
A = { } 

Coba perhatikan himpunan-himpunan di bawah ini, untuk mencari tahu pengertian dari himpunan kosong.

O = himpunan kucing yang bertelur.

P = himpunan bilangan ganjil yang habis dibagi 2.

R = himpunan nama hari yang berawalan huruf “Q”

Dari contoh di atas, bisakah kamu menentukan berapa banyak anggota-anggota dari himpunan O, P dan juga R? 

Jika kamu perhatikan, himpunan himpunan tersebut tidak memiliki anggota. Himpunan himpunan seperti itu disebut dengan himpunan kosong yang jika dilambangkan, akan dilambangkan dengan { } atau Ø .

Nah, dapatkah kamu menyebutkan contoh-contoh himpunan kosong lainnya?

Kamu bisa dengan mudah menyebutkan contoh himpunan maupun menjawab soal tersebut dengan mengikuti Platform Alef dari Alef Education. Penasaran kan apa itu Platform Alef? 

Platform Alef merupakan platform pembelajaran online dari Alef Education yang bergerak di bidang pendidikan, isi konten platform ini membahas matematika khusus siswa MTs/ SMP kelas 7, 8 dan 9 serta bahasa Arab untuk siswa tingkat MTs/SMP dan MA/SMAsecara gampang, asyik dan menyenangkan. Platform Alef sendiri banyak menyajikan video pembelajaran singkat untuk membantu kita lebih memahami matematika, juga dilengkapi permainan interaktif untuk menguji pengetahuan serta kuis-kuis latihan untuk membantu kita lulus ujian. Bagaimana sih cara mendapatkan akses Platform Alef? Caranya sangat mudah, cukup memberi tahu guru madrasah/sekolahmu tentang Platform Alef supaya mereka bisa mendapatkan kode akses  di alef.co.id atau melalui Alef Success Coach di wilayahmu.