



Mari Ketahui Operasi Hitung Aljabar: Rumus dan Caranya

Untuk mempelajari aljabar, kamu nggak cuma harus tahu sifat-sifat dalam aljabar tapi juga operasi hitung aljabar. Mulai dari penjumlahan hingga penghitungan pangkat dalam aljabar.
Sebelum itu, pastikan dulu kamu paham dasar-dasar aljabar ya. Mulai dari variabel, konstanta, koefisien dan suku. Tanpa pemahaman tersebut, kamu akan susah mempelajari aljabar.
Lebih lengkapnya, cek informasi berikut ini ya.
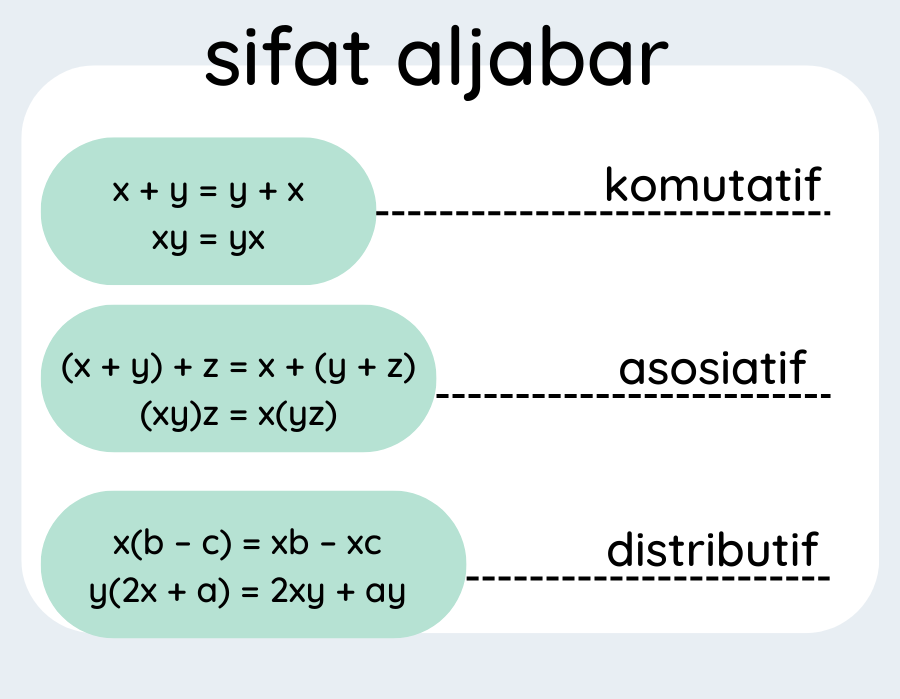
Dalam aljabar, terdapat sifat aljabar dan operasi hitungnya. Kamu wajib paham dulu sifat-sifatnya setelah itu, kamu bisa memahami operasi hitung aljabar.
Pada operasi hitung aljabar, terdapat beberapa hal yang harus kamu perhatikan dan pahami. Setelah itu, kamu bisa mencoba untuk mengerjakan soal persamaan aljabar termasuk soal cerita.
Dalam penjumlahan dan pengurangan aljabar hanya ada penjumlahan dan pengurangan dengan variabel sejenis.
Misalnya, 2x + 2xy+5x. Maka yang bisa kamu tambahkan atau jumlahkan hanya 2x dan 5x sehingga hasilnya adalah 7x + 2xy. 2xy tidak bisa kamu jumlahkan karena punya variabel yang berbeda, yaitu xy.
Sedangkan untuk pengurangan, kita ambil contoh ini, 4y – 2x -5y = -y – 2x. Di contoh tersebut, ada 2 variabel yaitu x dan y. Untuk pengurangan, kamu hanya bisa mengurangkan 4y – 5y sehingga hasilnya adalah -y – 2x.
Jadi, ketika kamu melihat persamaan aljabar, maka kamu harus melihat bagian variabelnya lebih dahulu. Cek, apakah ada yang sama dan bisa kamu jumlahkan/kurangkan atau tidak.

Berbeda dengan pengurangan dan penjumlahan, dalam perkalian aljabar, kamu bisa mengalikan semua variabel. Hal yang perlu kamu perhatikan adalah tanda kurungnya. Tanda kurung ini kerap kali mengecoh sehingga hasil persamaan aljabar pun menjadi salah.
Pada perkalian aljabar, terdapat perkalian antar suku. Bisa antara 1 suku dengan 2 suku, 1 suku dengan 1 suku, 2 suku dengan 2 suku. Agar lebih paham, kamu bisa simak bentuk umum dari perkalian aljabar berikut.
Contohnya, 2x(x-2y)=2x2-4xy. Kamu bisa mengalikan antara 2x dengan x dan 2x dengan 2y sehingga hasilnya adalah 2x2 – 4xy.
Bagaimana jika pengalian dengan lebih dari 2 suku?
Misalnya 4a(2ab-ab2-4ab).
Agar lebih mudah untuk menghitung, kamu bisa menggeser dulu -4ab ke dekat 2ab lalu kamu hitung terlebih dahulu. Seperti ini 4a((2ab-4ab)-ab2). Hasilnya adalah 4a(-2ab-ab2).
Dari persamaan 4a(-2ab-ab2), kamu bisa mulai menghitung.
-> (4a(-2ab))-(4aab2)
= -8a2b-4a2b2.
Paham ya sampai sini.
Untuk perkalian antara 2 suku dengan 2 suku, kamu bisa menggunakan konsep dasar sifat distributif (kamu bisa cek gambar di atas). Pahami dulu cara perkaliannya, karena banyak yang keliru dalam mengerjakannya.
Agar lebih paham, cek contoh berikut ini.
(x+2y)(x+3y)=x2+3xy+2xy+6y2=x2+5xy+6y2
Sampai sini paham ya?
Perlu kamu pahami kalau perkalian 2 suku dengan 2 suku bisa kamu artikan juga sebagai pengkuadratan suku dua. Misalnya (x+4)2. Artinya, persamaannya adalah (x+4)(x+4).
Penyelesaiannya, yaitu x2+4x+4x+16=x2+8x+16. Jadi, (x+4)2 = x2+8x+16.
Kamu mungkin bingung, bagaimana dengan perkalian 2 suku tapi berbeda, antara plus dan minus?
Untuk (x+y)(x-y), pada dasarnya cara perkaliannya sama. Jika kamu jabarkan, maka hasilnya:
x(x-y)+y(x-y)=x2-xy+xy-y2
= x2–y2
Jadi, (x+y)(x-y) = x2–y2.
Biar kamu lebih paham, cek contoh berikut ini
(x+2)(x-2) = x2-2x+2x-y2
= x2-4.
Sebagai catatan, biar kamu lebih mudah untuk mengerjakan perkalian selisih kuadrat adalah, kamu harus tahu bentuk kuadrat suatu bilangan.
Misalnya 32 = 9. Dengan cara ini, kamu tidak perlu terlalu pusing jika menemui soal selisih 2 kuadrat terutama jika tidak ada kalkulator.
Pada dasarnya, konsep pembagian aljabar sama dengan perkalian. Namun, ada beberapa hal yang perlu kamu perhatikan, yaitu:
Kalau kamu masih bingung, cek contoh pembagian berikut ini.
Bagaimana jika bentuknya adalah pecahan?
Agar kamu lebih mudah memahami, cek contoh ini. 2x4y3x2y2= (21)x4-2y3-2 = 2x2y
Jika kamu menguasai pembagian pecahan, walaupun bentuknya aljabar sekalipun, kamu akan lebih mudah memahami pembagian pecahan aljabar.
Sampai sini, paham ya?
Coba kamu flashback saat masa-masa SD. Di SD kamu sudah mempelajari tentang FPB. Kaitannya dengan aljabar adalah FPB akan digunakan dalam faktorisasi aljabar.
Jadi, kalau kamu ingat-ingat lupa, coba buka dulu materi FPB ya.
Faktorisasi aljabar ini sendiri fungsinya untuk menyatakan persamaan aljabar menjadi bentuk perkalian aljabar serta faktorisasinya.
Buat ‘memanggil’ memori matematika kamu, coba perhatikan contoh dengan variabel berikut tentang FPB dalam aljabar.
Misalnya, 18ab2, maka kita perlu membuat faktorisasi prima bentuk aljabarnya, yaitu 2 9 a b2 = 2 32 a b2.
Masih kurang paham? Coba perhatikan contoh berikut.
Berapa FPB dari 6a2 dan 12a3b2?
Pertama, kita buat faktorisasinya dulu:
6a2 = 2 3 a2
12a3b2= 22 3 a3 b2
Dari persamaan tersebut, cari faktor yang paling kecil dan jawabannya adalah 2 3 a2 = 6a2.
Sekarang, coba perhatikan faktorisasi dari 6a2 – 12a3b2!
FPB dari keduanya adalah 6a2. Maka kita keluarkan 6a2 menjadi 6a2(1-2ab2).
Kenapa (1-2ab2) dibiarkan saja? Tidak difaktorisasi? Karena 1 dan 2ab2 memang tidak bisa kamu faktorisasikan.
Maka hasil faktorisasi dari 6a2 – 12a3b2 adalah 6a2(1-2ab2).
Sesuai namanya, faktorisasi kuadrat akan menggunakan pangkat 2. Bentuk umumnya adalah ax2+bx+c.
Biar lebih paham, simak contoh persamaan x2+5x+6.
Dari persamaan tersebut, kamu bisa jabarkan menjadi x2+(3+2)x+(3 × 2)=(x+3)(x+2).
Kenapa hasilnya ada 3 dan 2?
Untuk menjabarkan, bagian 5x+6 kamu bisa berpikir 2 angka yang jika ditambah hasilnya adalah 5 dan jika dikali hasilnya adalah 6. Kedua angka tersebut adalah 3 dan 2. Angka tersebut jika kamu tambah hasilnya adalah 5 dan jika kamu kali hasilnya adalah 6.
Dari sini sudah ada pencerahan ya?
Cara yang sama juga bisa kamu terapkan jika persamaannya mengandung nilai negatif atau minus. Misalnya x2-6x+9.
Kita abaikan dulu nilai negatif di depan angka 6 biar kamu lebih mudah untuk menghitung. Sehingga persamaannya adalah x2+(-6x)+9.
Sekarang, angka berapa yang bisa kamu dapatkan jika ditambahkan hasilnya adalah -6 dan jika kamu kalikan hasilnya adalah 9? Yup! Jawabannya adalah -3.
Kenapa -3? Karena ketika negatif kamu kalikan dengan negatif, hasilnya adalah positif. Ingat rumusnya ya.
Jadi, hasil persamaan aljabar x2-6x+9=(x-3)(x-3).
Untuk membantu kamu lebih memahami aljabar, ada beberapa contoh soal, termasuk soal cerita.
Contoh Soal
Hasilnya adalah x-2b+10.
Jawabannya adalah 3x3yx =3x3-2y = 3x2y.
Hasilnya, jika apel = x dan jeruk = y, maka 5 apel dan 4 buah jeruk adalah 5x+4y=20.000.
Jawaban yang tepat adalah, (2(-2x))+(27)=-4x+14.
Hasilnya, ((-9)+10x)+(y+(-5y))=x-4y.
Dodi memiliki uang Rp50.000 dan uang tersebut ia gunakan untuk membeli 5 kg jeruk dan 6 kg apel. Harga 1 kg jeruk adalah 2 kali harga 1 kg apel. Lalu, berapa harga buah jeruk dan apel per kilo?
Jawaban,
Jika harga apel adalah x, maka harga jeruk adalah 2x karena harga per kg 2 kali lebih mahal dari apel.
Persamaannya adalah 5 jeruk + 6 apel = Rp50.000
= 5(2x)+6(x)=50.000=10x+6x=50.000.
16x=50.000
x = 3.125.
Jadi, x atau harga apel per kilo sebesar Rp3.125. Sedangkan harga jeruk per kg adalah 2x = 2(3.125) = Rp6.250.
Kakak punya kebun cabe berbentuk persegi dan Dedek punya kebun tomat berbentuk persegi panjang. Ukuran panjang dari kebun dedek 20 meter lebih panjang dari milik Kakak. Lebarnya adalah 10 meter lebih pendek dari panjang kebun milik Kakak. Jika keduanya memiliki luas kebun yang sama, berapa luas kebun cabe milik Kakak?
Jawabannya,
Jika panjang sisi kebun Kakak = x, maka panjang kebun tomat Dedek = x + 20 dan lebarnya adalah x – 10.
Kita harus mencari persamaan untuk luas kebun milik Dedek terlebih dahulu. Rumus luas persegi panjang adalah panjang x lebar. Maka,
Luas = (x+20)(x-10)
= x2-10x+20x-200=x2+10x-200.
Jadi luas kebun Dedek adalah x2+10x-200.
Karena Kakak memiliki kebun persegi, rumus luasnya adalah sisi × sisi atau sisi kuadrat. Dalam hal ini bisa kamu anggap sebagai x2. Jadi,
Luas kebun Kakak = luas kebun Dedek
x2=x2+10x-200
= 10x-200
200 = 10x
20 = x.
Jadi, nilai x atau sisi adalah 20.
Jika kamu pindah ke persamaannya untuk luas kebun Kakak, maka hasilnya adalah 20 × 20 = 400 meter persegi. Sedangkan jika kamu ingin mencari luas kebun Dedek, maka hitungannya adalah x2+10x-200=(20)2 +10(20)-200=400+200-200=400 meter persegi.
Paham ya sekarang?
Kalau kamu mau lebih paham lagi, kamu bisa meminta guru untuk meminta kode akses di alef.co.id atau hubungi Alef Success Coach. Di Alef, ada banyak materi serta pilihan soal dan jawaban yang bisa membantu kamu untuk mempelajari aljabar dengan lebih mudah.
Jadi, nggak ada alasan lagi buat kamu untuk malas belajar matematika aljabar. Semoga informasi seputar operasi hitung aljabar ini bisa membantu kamu belajar lebih baik lagi ya!
Baca Juga: Cara Belajar Matematika yang Efektif Dijamin Mudah
Dalam penjumlahan dan pengurangan aljabar hanya ada penjumlahan dan pengurangan dengan variabel sejenis. Misal, 2x + 2xy+5x. Maka yang bisa kamu tambahkan atau jumlahkan hanya 2x dan 5x sehingga hasilnya adalah 7x + 2xy. 2xy tidak bisa kamu jumlahkan karena punya variabel yang berbeda, yaitu xy. Untuk pengurangan, misalnya, 4y - 2x -5y = -y - 2x. Di contoh tersebut, ada 2 variabel yaitu x dan y. Untuk pengurangan, kamu hanya bisa mengurangkan 4y - 5y sehingga hasilnya adalah -y - 2x. Jadi, ketika kamu melihat persamaan aljabar, maka kamu harus melihat bagian variabelnya lebih dahulu. Cek, apakah ada yang sama dan bisa kamu jumlahkan/kurangkan atau tidak.
Ada tiga sifat-sifat Aljabar, yaitu: Sifat Komutatif, Sifat Asosiatif, dan Sifat Distributif
Dalam menyelesaikan perkalian aljabar, kamu bisa mengalikan semua variabel. Hal yang perlu kamu perhatikan adalah tanda kurungnya. Tanda kurung ini kerap kali mengecoh sehingga hasil persamaan aljabar pun menjadi salah. Pada perkalian aljabar, terdapat perkalian antar suku. Bisa antara 1 suku dengan 2 suku, 1 suku dengan 1 suku, 2 suku dengan 2 suku.